R.C. Beam Design - ACI 318-25

DESIGN OF R.C. BEAM - ACI 318-25

1.0 INPUT DATA

Material Properties (ACI 318-25)

f_c' = MPa Specified compressive strength of concrete [ACI 19.2.2]

f_y = MPa Specified yield strength of reinforcement [ACI 20.2.2]

γ_c = kN/m³ Unit weight of concrete

E_s = MPa Modulus of elasticity of steel

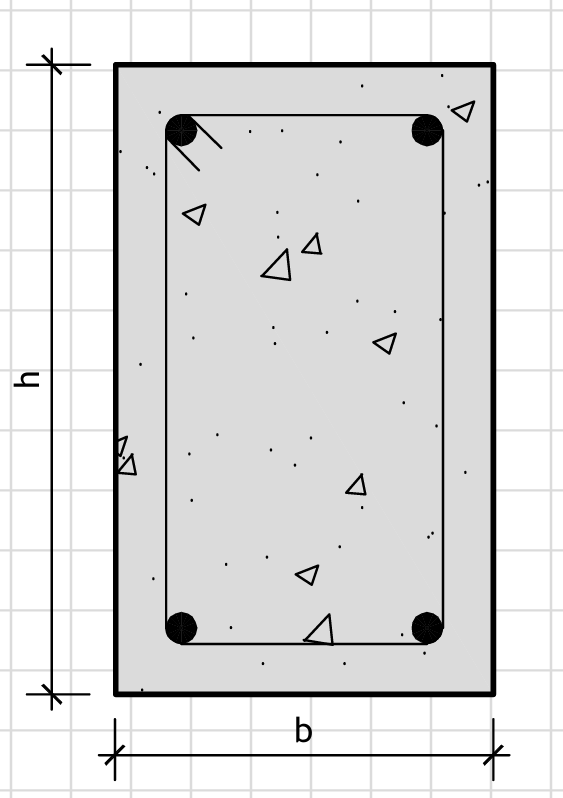
Figure 1: Geometry

RC Beam Dimensions

Load Factors and Strength Reduction Factors

φ_tension = Strength reduction factor for tension-controlled sections [ACI 21.2.2]

φ_shear = Strength reduction factor for shear [ACI 21.2.3]

λ = Modification factor for concrete density [ACI 19.2.4]

Section Dimensions

l = mm Clear span of beam [ACI 8.7]

h = mm Overall depth of beam

b = mm Width of beam

Loads

w_D = kN/m Service dead load

w_L = kN/m Service live load

M = kN·m Factored moment at midspan

V_u = kN Factored shear at support

M_a = kN·m Service moment for deflection check

Assumed Reinforcement

c_c = mm Clear cover to reinforcement [ACI 20.6]

φ_main = mm Main bar diameter

n_main = Number of main bars

φ_comp = mm Compression bar diameter (if needed)

n_comp = Number of compression bars (if needed)

φ_stirrup = mm Stirrup bar diameter

s = mm Stirrup spacing

c_agg,max = mm Maximum aggregate size [ACI 26.4.2.1]

2.0 CALCULATIONS

2.1 Design for Flexure

Effective depth to tension steel

d = h − c_c − φ_stirrup − φ_main/2

d = 450 - 40 - 10 - 20/2 = 380.00 mm

Effective depth to compression steel

d_' = c_c + φ_comp/2

d_' = 40 + 16/2 = 48.00 mm

Provided tension reinforcement

A_s,prov = n_main·(φ_main/2)²·π

A_s,prov = 3×(20/2)²×π = 942.48 mm²

ρ = A_s,prov/(b·d)

ρ = 942.48/(250×380) = 0.0099

Check minimum reinforcement requirement [ACI 9.6.1.2]

ρ_min = max(3·√(f_c')/f_y, 200/f_y) Units in psi

ρ_min = max(3×√(4352)/60924, 200/60924) = 0.0018

check_ρ_min = OK (ρ = 0.0099 ≥ ρ_min = 0.0018)

Check maximum reinforcement limit [ACI 9.6.2.1]

β₁ = 0.85 (for f'c ≤ 30 MPa) For normal-weight concrete [ACI 22.2.2.4.3]

ρ_b = 0.85·β₁·f_c'/f_y · E_s/(E_s + f_y) Balanced reinforcement ratio

ρ_b = 0.85×0.85×30/420 × 200000/(200000+420) = 0.0025

ρ_max = 0.85·ρ_b Maximum reinforcement for tension-controlled sections

ρ_max = 0.85×0.0025 = 0.0021

check_ρ_max = FAIL (ρ = 0.0099 ≤ ρ_max = 0.0021)

Check if compression steel is required

Compression steel IS required (ρ > ρ_max)

Calculate compression steel requirement

ρ_comp = ρ − ρ_max

ρ_comp = 0.0099 - 0.0021 = 0.0078

A_s',req = ρ_comp·b·d

A_s',req = 0.0078×250×380 = 740.63 mm²

Provide compression bars (e.g. 2No.#16)

A_s',prov = n_comp·(φ_comp/2)²·π

A_s',prov = 2×(16/2)²×π = 402.12 mm²

check_A_s' = FAIL (A_s',prov = 402.12 < A_s',req = 740.63 mm²)

Calculate nominal moment strength with compression steel

a = A_s,prov·f_y/(0.85·f_c'·b)

a = 942.48×420/(0.85×30×250) = 62.42 mm

M_n = A_s,prov·f_y·(d − a/2)

M_n = 942.48×420×(380 - 62.42/2) = 136082976 N·mm

Calculate design moment strength

φ_Mn = φ_tension·M_n

φ_Mn = 0.9×136082976 = 122474.68 kN·mm = 122.47 kN·m

Check flexural strength

check_flexure = OK (φ_Mn = 122.47 ≥ M = 112.50 kN·m)

2.2 Design for Shear - ENHANCED ACI 318-25 PROVISIONS

Shear demand

v_u = V_u/(b·d)

v_u = 75000/(250×380) = 0.789 MPa

Concrete shear strength [ACI 318-25 Section 22.5.5.1]

v_c = 0.17·λ·λ_s·√(f_c')·√(1 + β_c) For beam, β_c = 0

λ_s = √(2/(1 + 0.004·d)) Size effect factor [ACI 22.5.5.1.3]

λ_s = √(2/(1 + 0.004×380)) = 0.97

v_c = 0.17×λ×λ_s×√(f_c')

v_c = 0.17×1.0×0.97×√(30) = 0.90 MPa

v_c,min = λ·√(f_c') Minimum concrete shear stress [ACI 22.5.5.2]

v_c,min = 1.0×√(30) = 5.477 MPa

v_c,design = max(v_c, v_c,min)

v_c,design = max(0.90, 5.477) = 5.477 MPa

Design concrete shear strength

φ_v·v_c,design = φ_shear·v_c,design

φ_v·v_c,design = 0.75×5.477 = 4.108 MPa

Design for shear reinforcement

check_shear = OK (v_u = 0.789 ≤ φ_v·v_c,design = 4.108 MPa)

2.3 Serviceability - Deflection Check

Effective moment of inertia [ACI 24.2.3.5]

I_e = min[(M_cr/M_a)³·I_g + [1 − (M_cr/M_a)³]·I_cr, I_g]

M_cr = f_r·I_g/(y_t)

f_r = 0.62·λ·√(f_c') Modulus of rupture

f_r = 0.62×1.0×√(30) = 3.40 MPa

I_g = b·h³/12

I_g = 250×450³/12 = 3785156250 mm⁴

y_t = h/2 Distance from centroid to extreme tension fiber

y_t = 450/2 = 225 mm

M_cr = 3.40×3785156250/225 = 57156406 N·mm = 57.16 kN·m

I_cr = n·A_s·(d − c)² + b·c³/3

c = √[(n·A_s)² + 2·n·A_s·d] − n·A_s

E_c = 4700·√(f_c')·√(γ_c/23.5)

E_c = 4700×√(30)×√(24/23.5) = 25740 MPa

n = E_s/E_c

n = 200000/25740 = 7.77

c = √[(7.77×942.48)² + 2×7.77×942.48×380] − 7.77×942.48 = 39.16 mm

I_cr = 7.77×942.48×(380-39.16)² + 250×39.16³/3 = 87709076 mm⁴

Service moment (user-provided for deflection check)

M_a = 78.13 (user input) kN·m

I_e = min((57.16/78.13)³×3785156250 + [1−(57.16/78.13)³]×87709076, 3785156250) = 87709076 mm⁴

Deflection calculation (simple span, uniformly distributed load)

Δ = 5·(w_D + w_L)·l⁴/(384·E_c·I_e)

Δ = 5×25×6000⁴/(384×25740×87709076) = 8.43 mm

Check deflection limits [ACI Table 24.2.2]

Allowable Δ = l/240 = 6000/240 = 25.00 mm

check_deflection = OK (Δ = 8.43 ≤ Allowable = 25.00 mm)

2.4 Crack Control [ACI 24.3]

Calculate z-factor for beam

z = β·h_c·√(d_c·A) [ACI 24.3.2]

β = d/(d_c) = 380/(40+10+20/2) = 4.75

h_c = c_c + φ_stirrup + φ_main/2

h_c = 40 + 10 + 20/2 = 60 mm

d_c = h_c

A = 2·d_c·(b/n_main)

A = 2×60×(250/3) = 10000 mm²

z = 4.75×60×√(60×10000) = 36898 N/mm

check_crack = FAIL (z = 36898 > 30000 N/mm for interior exposure)

2.5 Bar Spacing Requirements [ACI 25.2]

Minimum spacing requirements [ACI 25.2.1]

s_min = max(φ_main, 1.33·c_agg,max, 25 mm)

s_min = max(20, 1.33×19, 25) = 25.00 mm

check_s_min = OK (Spacing between bars ≥ 25.00 mm)

Maximum spacing for crack control [ACI 24.3.2]

s_max,crack = min(12×d_c, 300) mm For interior exposure with moderate corrosion risk

s_max,crack = 300.00 mm

check_s_max,crack = OK (Provide adequate spacing for crack control)

Stirrup spacing check [ACI 9.7.6.2]

s_max,stirrup = min(16×φ_main, d/2, 300) mm

s_max,stirrup = 190.00 mm

check_s_stirrup = OK (s = 150 ≤ s_max,stirrup = 190.00 mm)

* OUTPUT SUMMARY *

Design Results

Effective depth, d = 380.00 mm

Provided tension steel, A_s,prov = 942.48 mm²

Required compression steel, A_s',req = 740.63 mm²

Provided compression steel, A_s',prov = 402.12 mm²

Reinforcement ratio, ρ = 0.0099

Design moment strength, φ_Mn = 122.47 kN·m

Flexural strength check: OK

Compression steel check: FAIL - Increase compression steel

Shear stress, v_u = 0.789 MPa

Design concrete shear strength, φ_v·v_c,design = 4.108 MPa

Shear capacity check: CHECK

Calculated deflection, Δ = 8.43 mm

Allowable deflection = 25.00 mm

Deflection check: OK

Crack control check: FAIL - Increase cover or reduce spacing

Bar spacing check: OK

RESULTS

DESIGN FAILS - INCREASE COMPRESSION STEEL AND IMPROVE CRACK CONTROL