🏗️ Beam Analysis Calculators

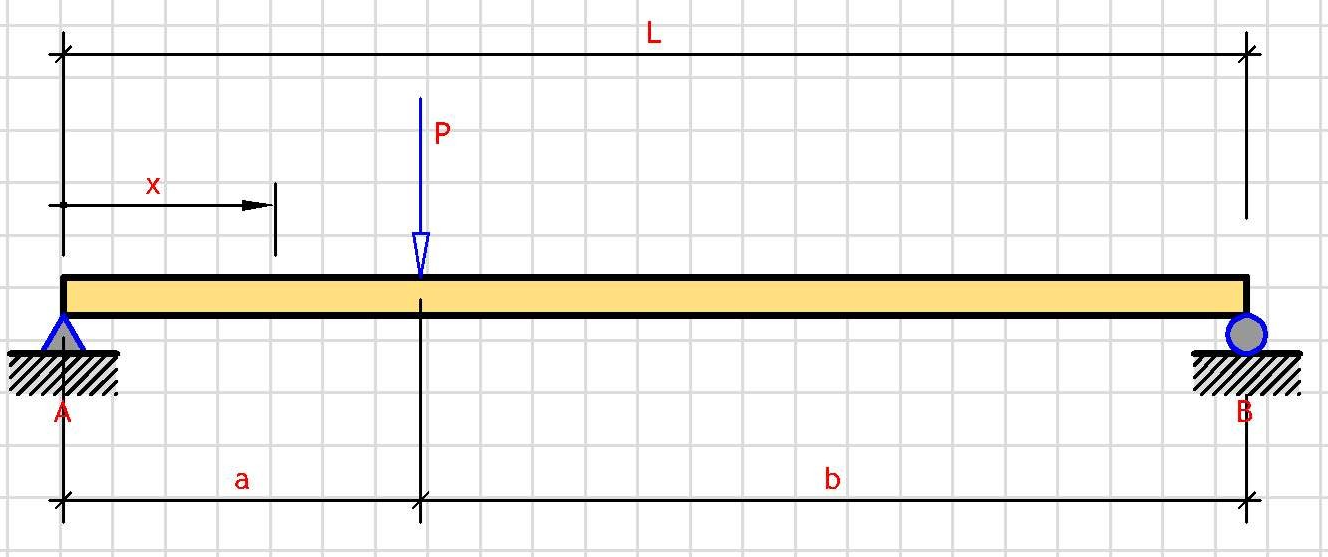
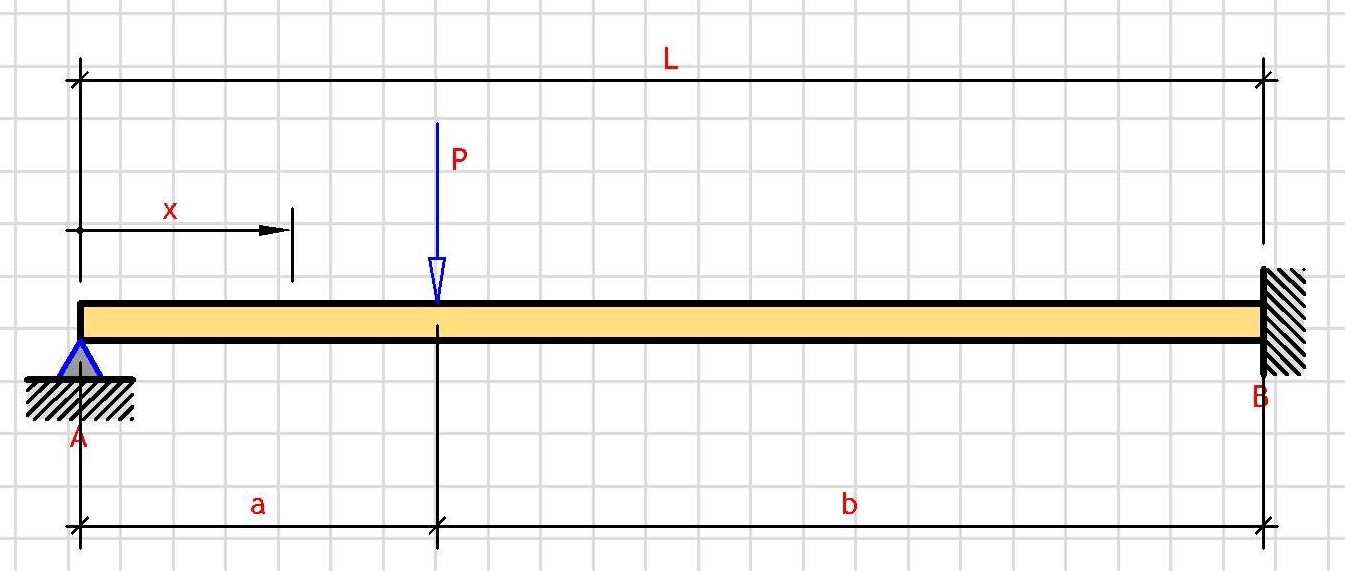
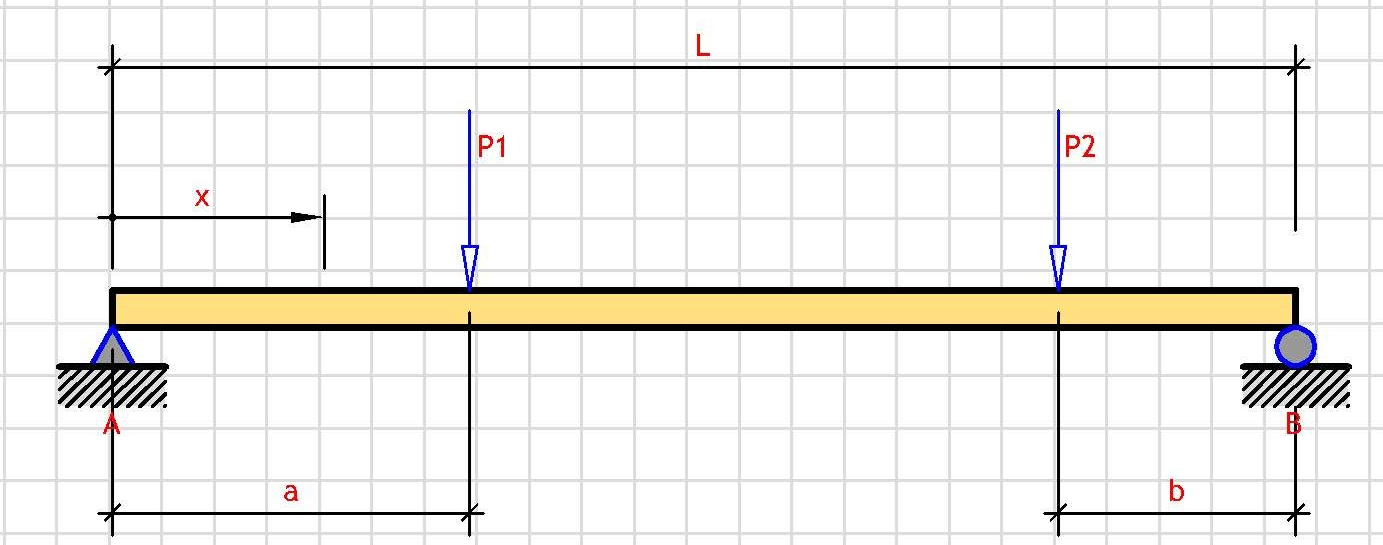
Support Reactions:

V_A = [P₁·(L-a) + P₂·b]/L

V_B = [P₁·a + P₂·(L-b)]/L

Shear Force V(x):

if(x ≤ a) → V_A

if(a < x ≤ L-b) → V_A - P₁

if(x > L-b) → -V_B

Bending Moment M(x):

if(x ≤ a) → V_A·x

if(a < x ≤ L-b) → V_A·x - P₁·(x-a)

if(x > L-b) → V_B·(L-x)

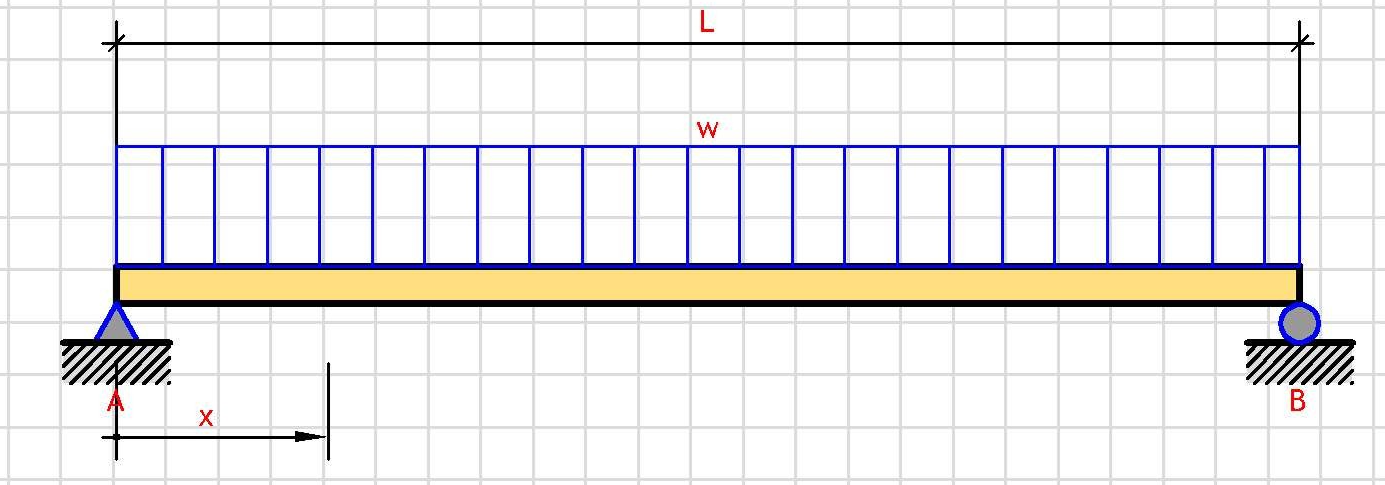
Support Reactions:

V_A = w·L/2

V_B = w·L/2

Shear Force V(x):

V(x) = w·(L/2 - x)

Bending Moment M(x):

M(x) = w·x/2·(L - x)

Deflection δ(x):

δ(x) = -w·x·(L³-2·L·x²+x³)/(24·E·I)

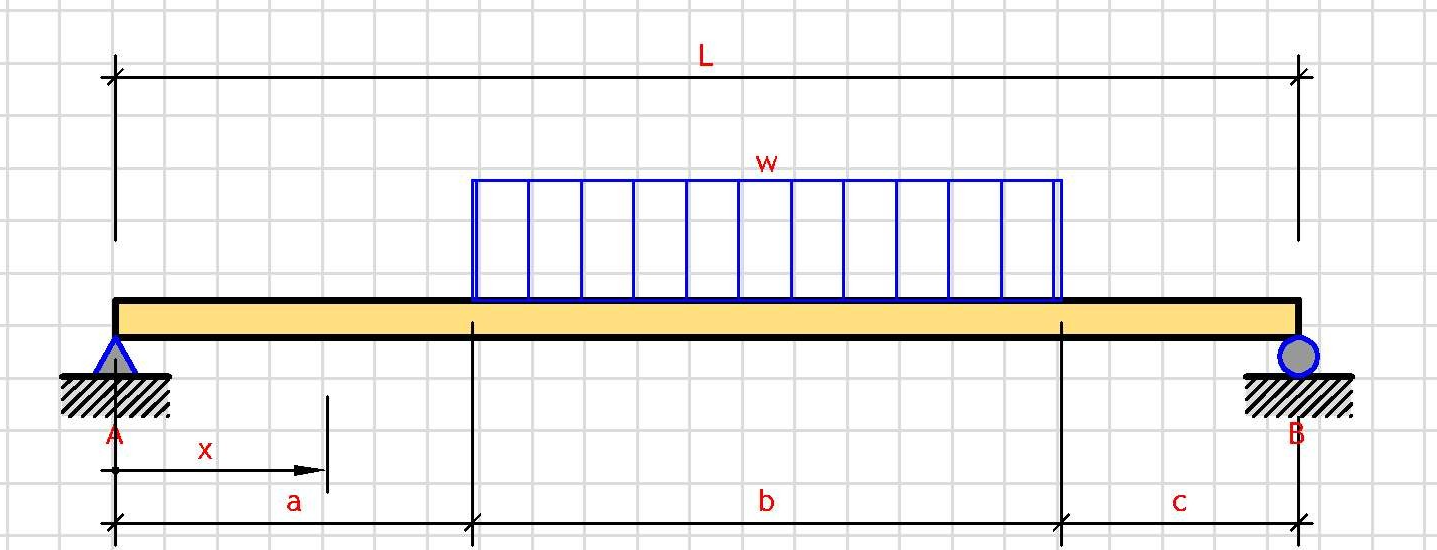
Support Reactions:

c = L - a - b

V_A = w·b·(2c + b)/(2L)

V_B = w·b·(2a + b)/(2L)

Shear Force V(x):

if(x ≤ a) → V_A

if(a < x ≤ a+b) → V_A - w·(x-a)

if(x > a+b) → -V_B

Bending Moment M(x):

if(x ≤ a) → V_A·x

if(a < x ≤ a+b) → V_A·x - (w/2)·(x-a)²

if(x > a+b) → V_B·(L-x)

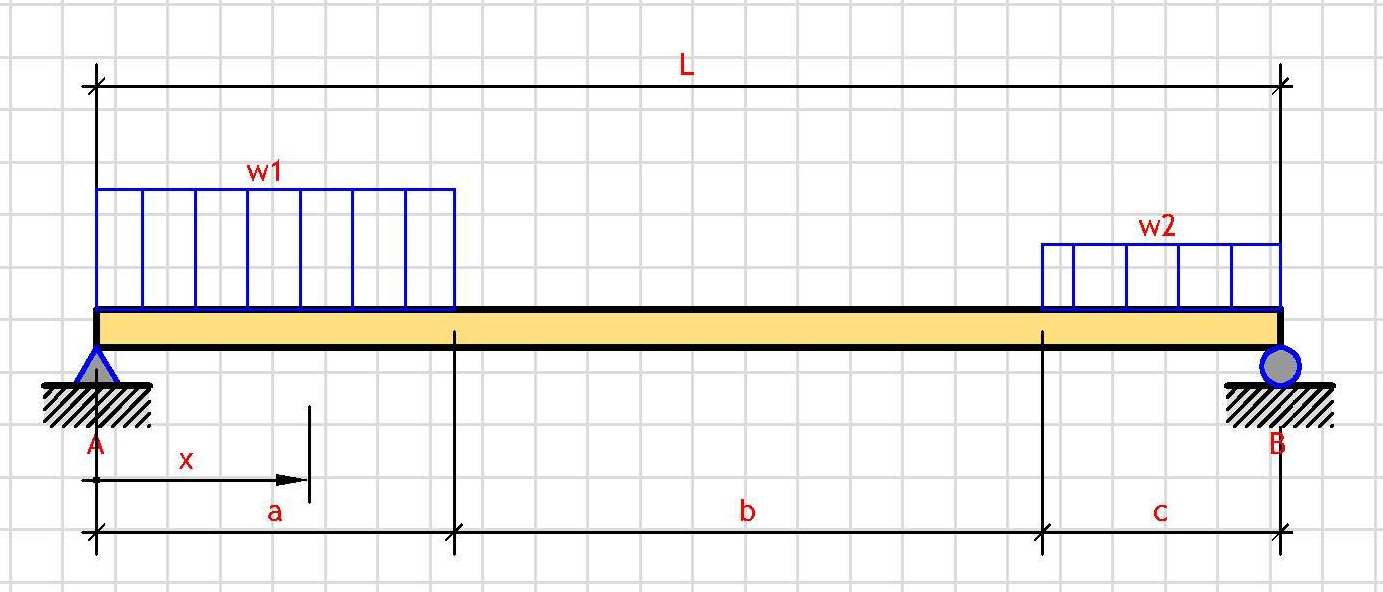
Support Reactions:

b = L - a - c

V_A = [w₁·a·(2L-a) + w₂·c²]/(2L)

V_B = [w₂·c·(2L-c) + w₁·a²]/(2L)

Shear Force V(x):

if(x ≤ a) → V_A - w₁·x

if(a < x ≤ a+b) → V_A - w₁·a

if(x > a+b) → -(V_B - w₂·(L-x))

Bending Moment M(x):

if(x ≤ a) → V_A·x - w₁·x²/2

if(a < x ≤ a+b) → V_A·x - w₁·a·(2x-a)/2

if(x > a+b) → V_B·(L-x) - w₂·(L-x)²/2

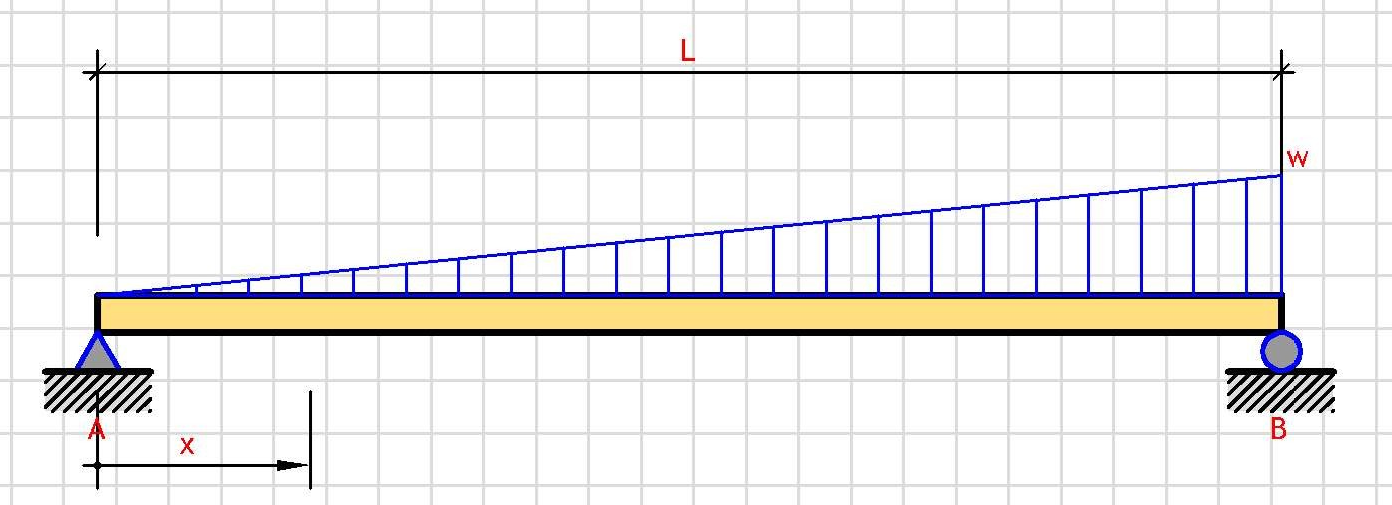
Total Load:

W = (1/2)·L·w

Support Reactions:

V_A = W/3

V_B = 2·W/3

Shear Force V(x):

V(x) = W/3 - W·x²/L²

Bending Moment M(x):

M(x) = (W·x)·(L² - x²)/(3·L²)

Deflection δ(x):

δ(x) = -W·x·(3·x⁴ - 10·L²·x² + 7·L⁴)/(180·E·I·L²)

(negative = downward)

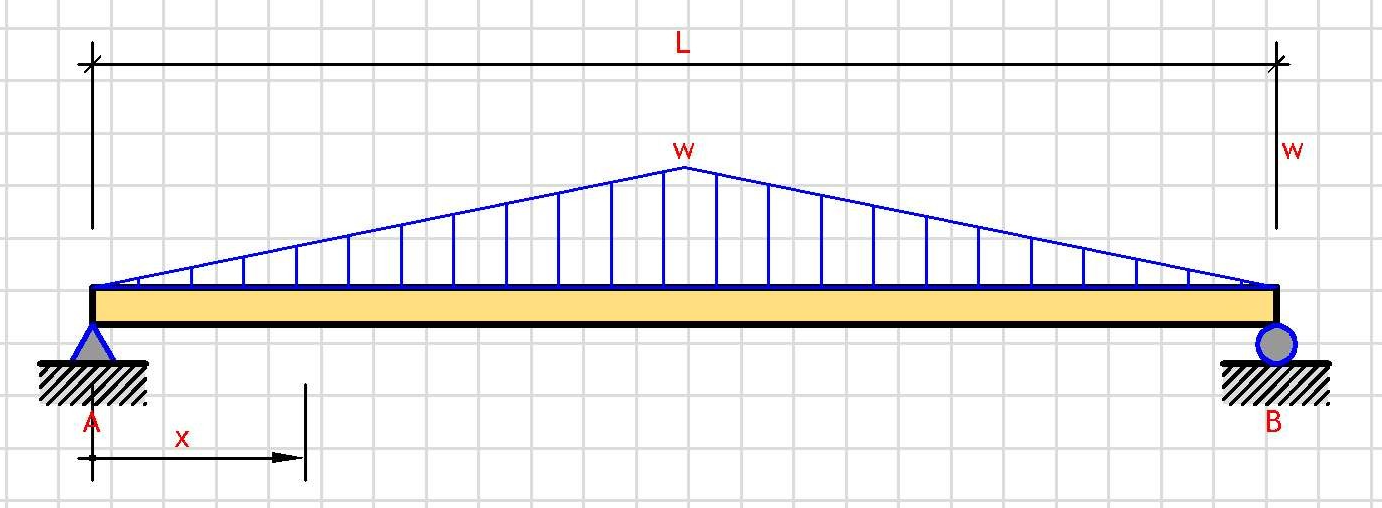
Total Load:

W = (1/2)·L·w

Support Reactions:

V_A = W/2

V_B = W/2

Shear Force V(x):

if(0 ≤ x ≤ L/2) → w·(L² - 4·x²)/(4·L)

if(x > L/2) → -w·(L² - 4·(L - x)²)/(4·L)

Bending Moment M(x):

if(0 ≤ x ≤ L/2) → (w·L·x/2)·(1/2 - 2·x²/(3·L²))

if(x > L/2) → (w·L·(L - x)/2)·(1/2 - 2·(L - x)²/(3·L²))

Deflection δ(x):

δ(x) = -W·x·(5·L² - 4·x²)²/(480·E·I·L²)

(negative = downward)

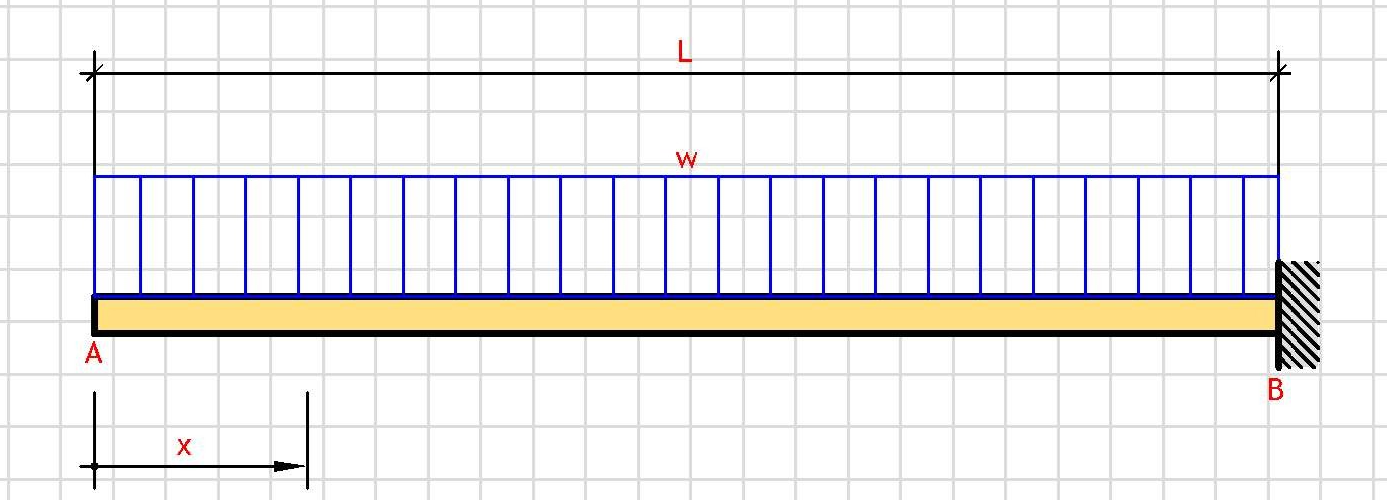
Support Reaction:

V = w·L

Shear Force V(x):

V(x) = w·x

Bending Moment M(x):

M(x) = w·x²/2

Deflection δ(x):

δ(x) = -w·(x⁴ - 4·L³·x + 3·L⁴)/(24·E·I)

(negative = downward)

Distance Parameters:

b = L - a

Support Reaction:

V = P

Shear Force V(x):

if(0 ≤ x ≤ a) → 0

if(x > a) → V

Bending Moment M(x):

if(0 ≤ x ≤ a) → 0

if(x > a) → P·(x - a)

Deflection δ(x):

if(0 ≤ x ≤ a) → -P·b²·(3·L - 3·x - b)/(6·E·I)

if(x > a) → -P·(L - x)²·(3·b - L + x)/(6·E·I)

(negative = downward)

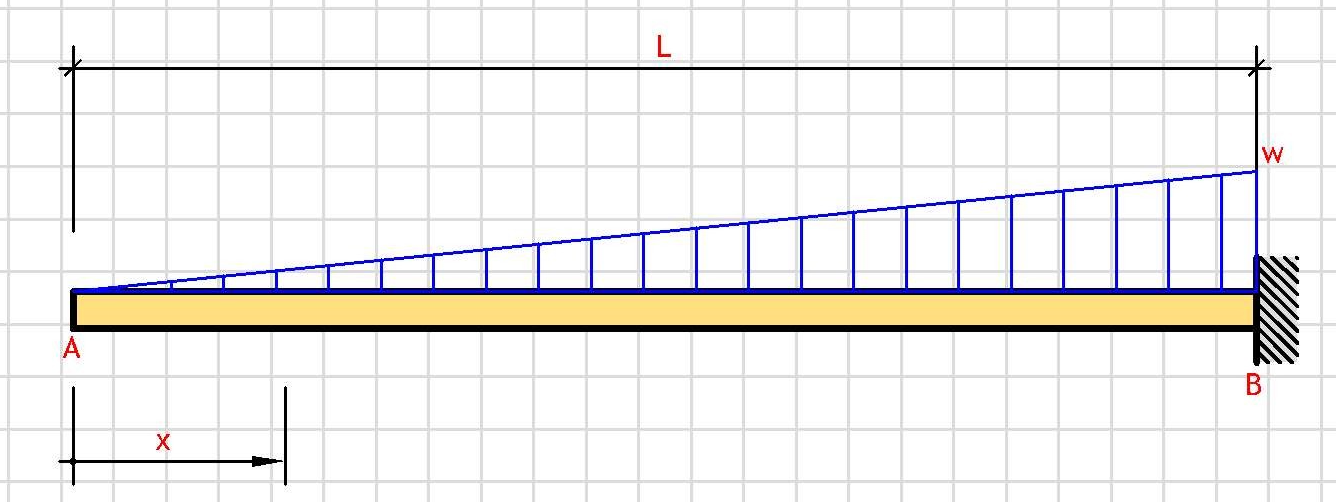
Total Load:

W = (1/2)·L·w

Support Reaction:

V = w·L/2

Shear Force V(x):

V(x) = w·x²/(2·L)

Bending Moment M(x):

M(x) = w·x³/(6·L)

Deflection δ(x):

δ(x) = -W·x²·(x⁵ + 5·L⁴·x + 4·L⁵)/(60·E·I·L²)

(negative = downward)

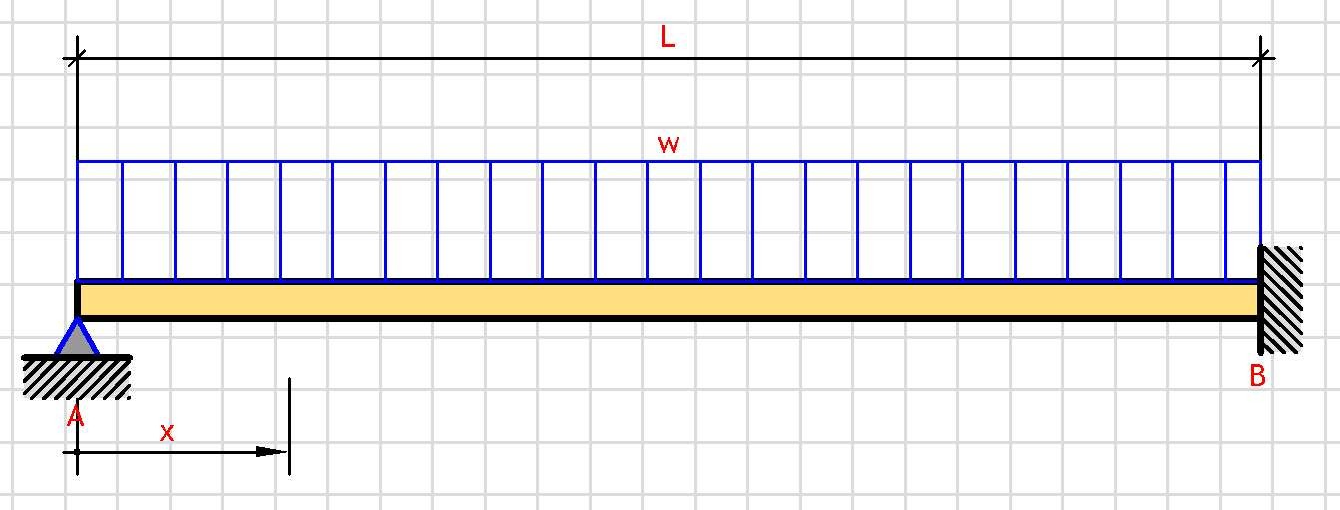
Support Reactions:

V_A = 3·w·L/8

V_B = 5·w·L/8

Shear Force V(x):

V(x) = V_A - w·x

Bending Moment M(x):

M(x) = V_A·x - w·x²/2

Deflection δ(x):

δ(x) = -w·x·(L³ - 3·L·x² + 2·x³)/(48·E·I)

(negative = downward)

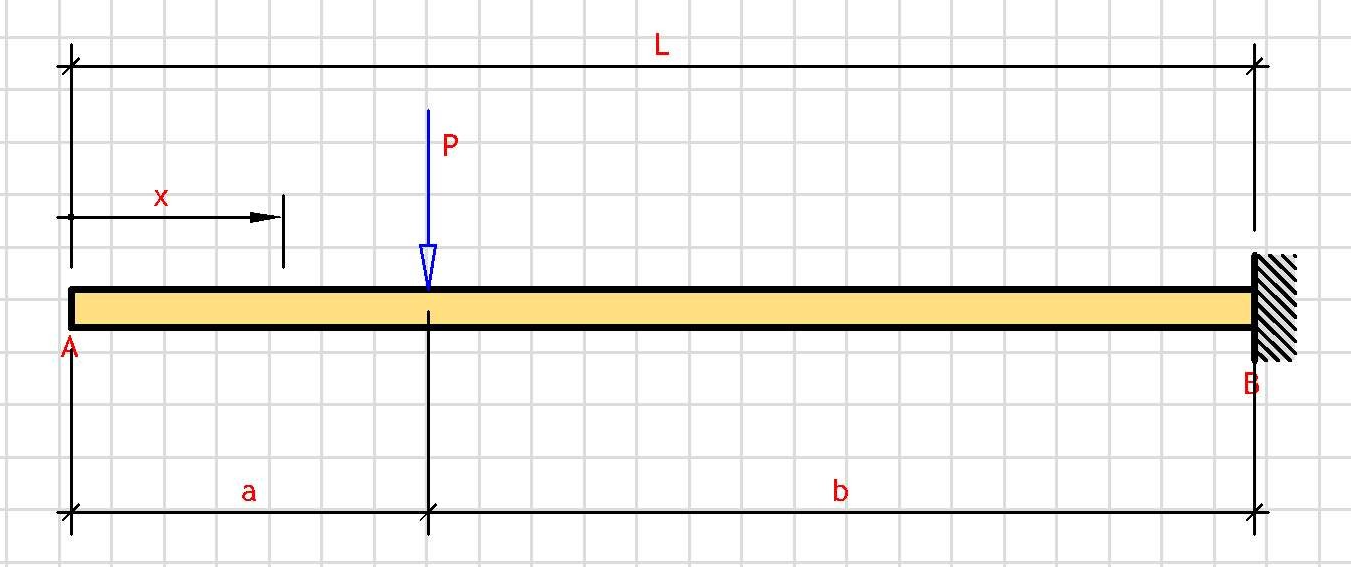
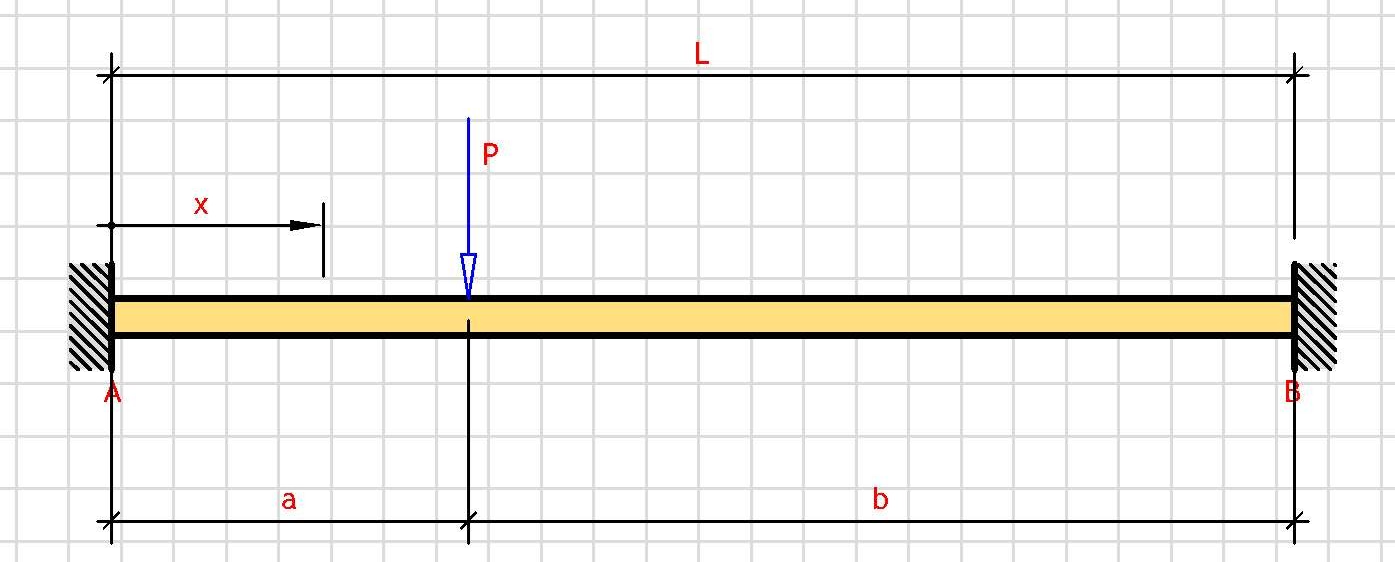
Distance Parameters:

b = L - a

Support Reactions:

V_A = P·b²·(a + 2·L)/(2·L³)

V_B = P·a·(3·L² - a²)/(2·L³)

Shear Force V(x):

if(0 ≤ x ≤ a) → V_A

if(x > a) → -V_B

Bending Moment M(x):

if(0 ≤ x ≤ a) → V_A·x

if(x > a) → V_A·x - P·(x - a)

Deflection δ(x):

if(0 ≤ x ≤ a) → -P·b²·x·(3·a·L² - 2·L·x² - a·x²)/(12·E·I·L³)

if(x > a) → -P·a·(L - x)²·(3·L²·x - a²·x - 2·a²·L)/(12·E·I·L³)

(negative = downward)

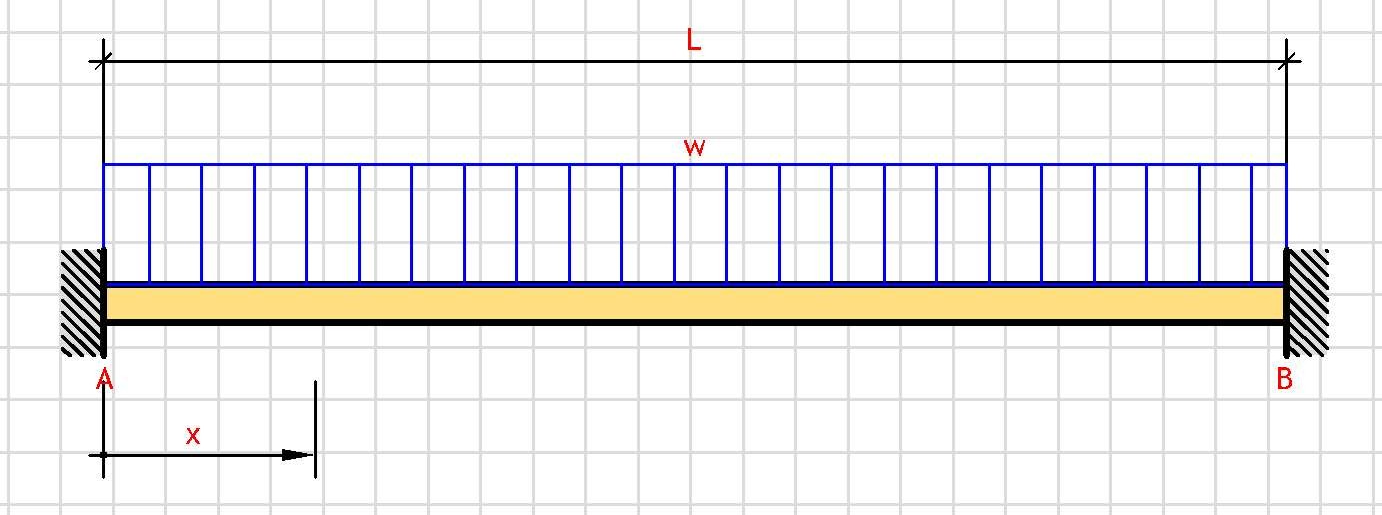
Support Reactions:

V_A = w·L/2

V_B = w·L/2

Shear Force V(x):

V(x) = w·(L/2 - x)

Bending Moment M(x):

M(x) = w·(6·L·x - L² - 6·x²)/12

Deflection δ(x):

δ(x) = -w·x²·(L - x)²/(24·E·I)

(negative = downward)

Distance Parameters:

b = L - a

Support Reactions:

V_A = P·b²·(3·a + b)/L³

V_B = P·a²·(a + 3·b)/L³

Shear Force V(x):

if(0 ≤ x ≤ a) → V_A

if(x > a) → -V_B

Bending Moment M(x):

if(0 ≤ x ≤ a) → V_A·x - P·a·b²/L²

if(x > a) → V_B·(L - x) - P·a²·b/L²

End Moments:

M_A = -P·a·b²/L²

M_B = -P·a²·b/L²

Deflection δ(x):

if(0 ≤ x ≤ a) → -(-V_A·x³/(6·E·I) - M_A·x²/(2·E·I))

if(x > a) → -(-V_A·x³/(6·E·I) - M_A·x²/(2·E·I) + P·(x - a)³/(6·E·I))

(negative = downward)

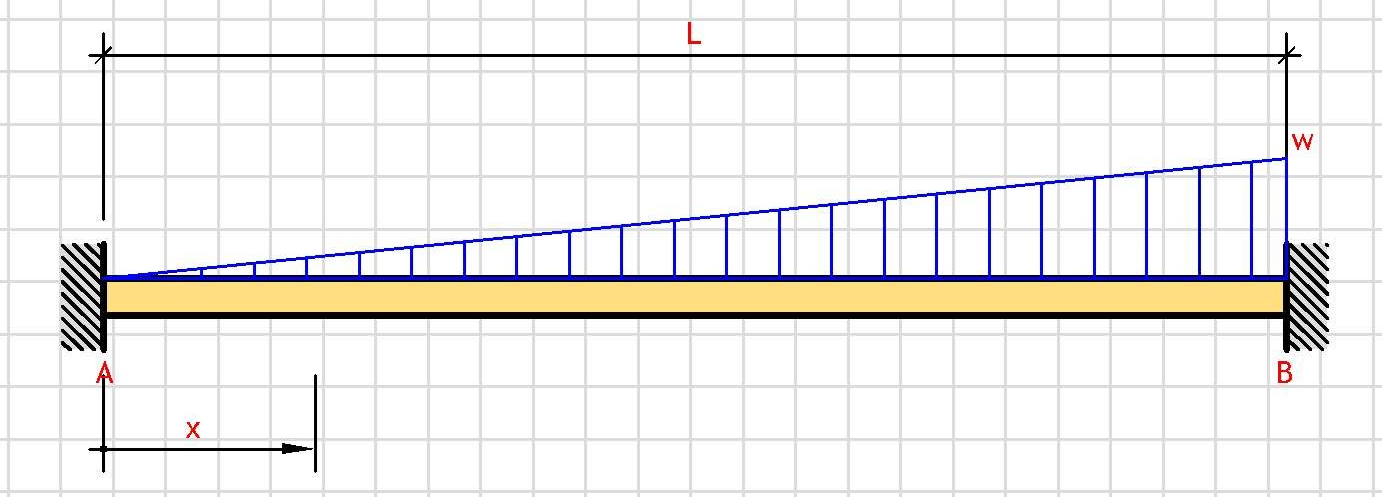
Support Reactions:

V_A = 3·w·L/20

V_B = 7·w·L/20

End Moments:

M_A = -w·L²/30

M_B = -w·L²/20

Shear Force V(x):

V(x) = w·(3·L² - 10·x²)/(20·L)

Bending Moment M(x):

M(x) = -w·(2·L³ - 9·L²·x + 10·x³)/(60·L)

Deflection δ(x):

δ(x) = -(-V_A·x³/(6·E·I) - M_A·x²/(2·E·I) + w·x⁵/(120·E·I·L))

(negative = downward)

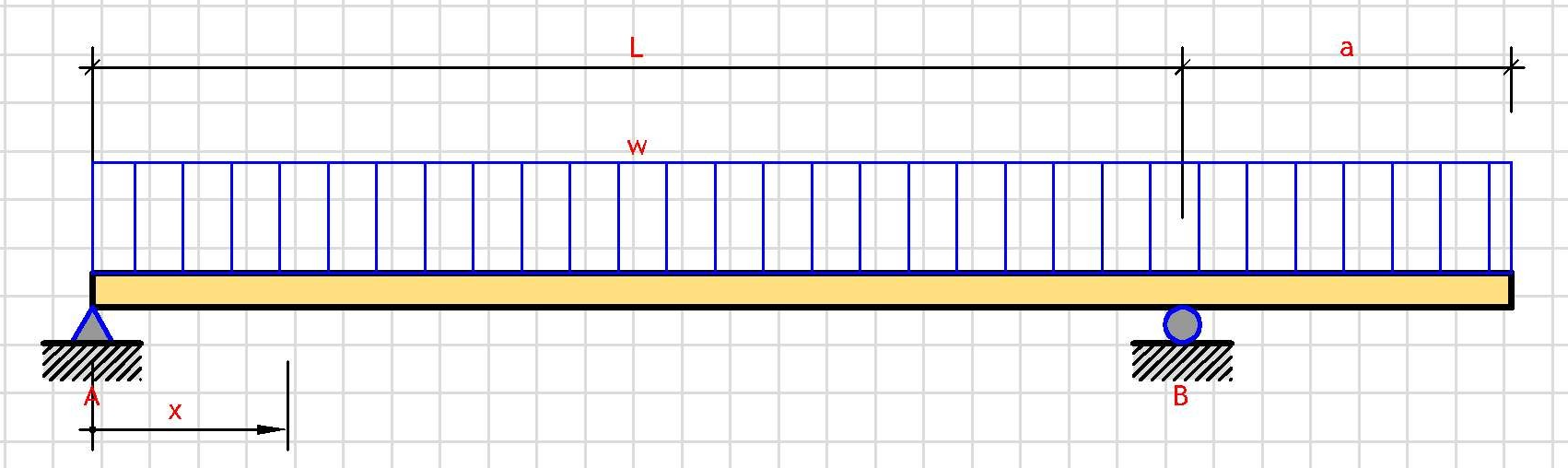
Support Reactions:

V_A = w·(L² - a²)/(2·L)

V_Bl = w·a (L-side)

V_Br = w·(L² + a²)/(2·L) (R-side)

V_B = V_Bl + V_Br

Shear Force V(x):

if(0 ≤ x ≤ L) → V_A - w·x

if(x > L) → w·(a - (x - L))

Bending Moment M(x):

if(0 ≤ x ≤ L) → w·x·(L² - a² - x·L)/(2·L)

if(x > L) → -w·(a - (x - L))²/2

Deflection δ(x):

if(0 ≤ x ≤ L) → -w·x·(L⁴ - 2·L²·x² + L·x³ - 2·a²·L² + 2·a²·x²)/(24·E·I·L)

if(x > L) → -w·(x - L)·(4·a²·L - L³ + 6·a²·(x - L) - 4·a·(x - L)² + (x - L)³)/(24·E·I)

(negative = downward)