COMPOSITE BEAM DESIGN CALCULATOR
Steel-Concrete Composite Beam Design
Steel-Concrete Composite Beam Design
Beam Geometry
L = m Span of the simply supported beam
S = m Beam spacing
Steel Beam Properties (H-Section)
D = mm Overall depth of steel beam
bf = mm Flange width
tf = mm Flange thickness
tw = mm Web thickness
As = cm² Steel section area
py = MPa Design strength of structural steel (S355)
Es = MPa Steel modulus of elasticity
Figure 1: Geometry
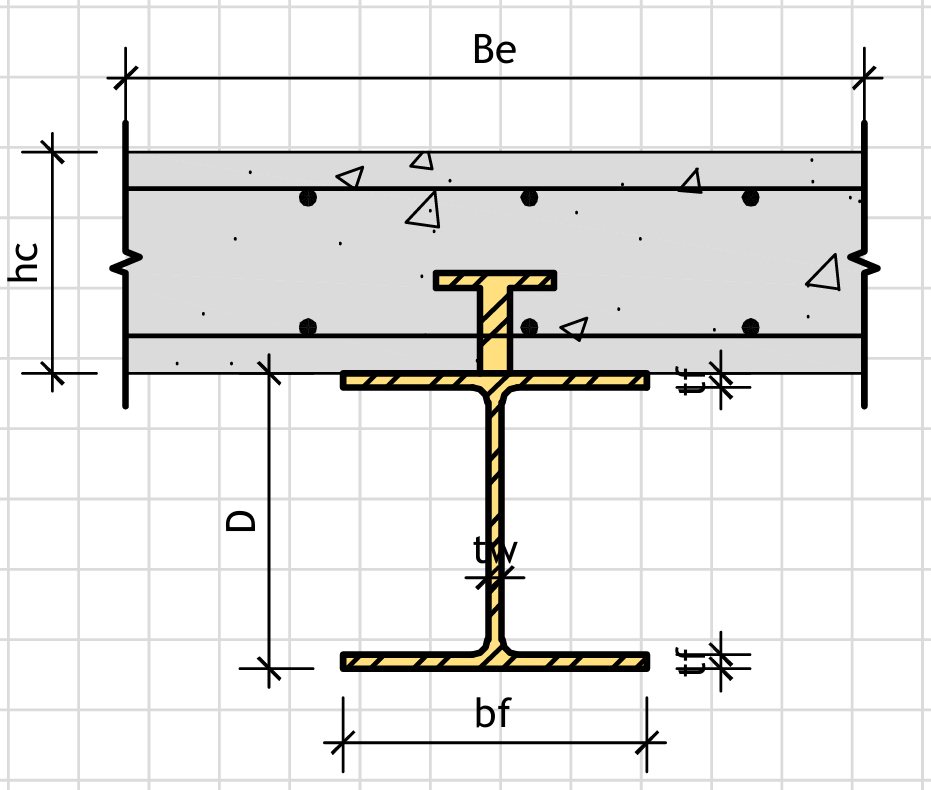
Composite Beam Dimensions
Concrete Slab Properties
hc = mm Total slab depth (decking + concrete)
tconc = mm Concrete topping thickness (above deck)
Be = mm Effective breadth of concrete flange
fcu = MPa Concrete cube compressive strength (C30)
γc = Partial safety factor for concrete
γconc_wt = kN/m³ Concrete density
Decking Properties
hd = mm Decking height
wd = kN/m² Decking self-weight
Shear Connector Properties (Headed Studs)
dstud = mm Stud diameter
hstud = mm Stud height
fu_stud = MPa Stud ultimate strength (Grade 450)
γv = Partial safety factor for shear connectors
nstuds = Provided number of studs
Loading (Characteristic values)
gk_fin = kN/m² Finishes
qk = kN/m² Imposed load
Partial Safety Factors for Loads
γf_g = Dead load factor
γf_q = Imposed load factor
dw = D - 2·tf = 378.2 mm Clear web depth
Is = 31234.5 cm⁴ Moment of inertia for steel section
gk_slab = 5.4 kN/m Slab self-weight (excluding decking)
wg_k = 8.24 kN/m Total characteristic dead load per meter
wq_k = 12.0 kN/m Total characteristic imposed load per meter
Effective Width of Concrete Flange
be = min(L/4; S) = 2.5 m Effective width
Aconc = be·tconc = 187500 mm² Effective concrete area
fcd = fcu/γc = 20.0 MPa Design strength of concrete
Nc = 0.85·fcd·Aconc = 3187.5 kN Concrete compression force capacity
Ns = As·py = 3503.9 kN Full steel tension force
a =
Ns/(0.85·fcd·be) Depth
of concrete stress block
z = D/2 + tconc - a/2
Lever arm
(N_c ≥ N_s)
' Case 1: PNA in concrete slab
M_p = N_s*z
"Check_PNA = In concrete slab"
(N_c < N_s)
' Case 2: PNA in steel beam
F_c = N_c' Compression in concrete
y_pna = (N_s - N_c)/(2*t_w*p_y) + (D - 2*t_f)/2' Depth of PNA relative to
top of web
M_p = F_c*(D/2 + t_conc - a/2) + p_y*A_s*(y_pna)' Simplified moment
capacity (requires careful
PNA calc)
"Check_PNA = In steel beam"
Mp = 1234.5 kN·m Plastic moment capacity
Flexural Resistance Check
M* = (γf_g·wg_k + γf_q·wq_k)·L²/8 = 287.7 kN·m Factored design moment
Moment Check: M*/Mp = 0.233
V* = (γf_g·wg_k + γf_q·wq_k)·L/2 = 115.1 kN Factored design shear
Av = D·tw = 3535.7 mm² Web shear area
Pv = 0.6·py·Av/1.1 = 691.8 kN Shear capacity
Shear Check: V*/Pv = 0.166
α = 0.2·(hstud/dstud) + 0.8 = 1.85 Alpha factor
Qp = 127.2 kN Stud shear resistance
Nreq_FSC = min(Ns; Nc)/Qp = 25.1 Required studs for FSC
Shear Connection Check: nstuds/Nreq_FSC = 0.797 PARTIAL SHEAR CONNECTION
Stage 1: Construction (Steel Beam Only)
wconstr_k = 8.24 kN/m Characteristic load during construction
δconstr = 5·wconstr_k·L⁴/(384·Es·Is) = 12.8 mm Deflection during construction
δconstr_limit = L/180 = 55.6 mm Construction deflection limit
Construction Deflection Check: δconstr/δconstr_limit = 0.230
Stage 2: Serviceability (Composite Action)
Ecm = 22200 MPa Short-term concrete modulus
me = Es/Ecm = 9.23 Short-term modular ratio
Icomp = 89456.3 cm⁴ Composite section moment of inertia
δimp_short = 5·wq_k·L⁴/(384·Es·Icomp) = 5.5 mm Short-term imposed deflection
δimp_limit = L/360 = 27.8 mm Imposed deflection limit
Imposed Deflection Check: δimp_short/δimp_limit = 0.198
Long-term Deflection (Creep)
φ = Creep coefficient (conservative)
me_lt = 27.69 Long-term modular ratio
Icomp_lt = 45623.1 cm⁴ Long-term composite moment of inertia
δfinal = 24.7 mm Total final deflection
δfinal_limit = L/250 = 40.0 mm Total deflection limit
Final Deflection Check: δfinal/δfinal_limit = 0.618
Capacities:
Design Flexural Capacity: 1234.5 kN·m
Design Shear Capacity: 691.8 kN
Required Studs for FSC: 25.1
Provided Studs: 20
Design Actions:
Factored Design Moment: 287.7 kN·m
Factored Design Shear: 115.1 kN
Construction Deflection: 12.8 mm
Final Deflection: 24.7 mm