CHS Capacity Check to EN1993-1-1

INPUTS

Section properties (mm)

D = mm Outer diameter

t = mm Wall thickness

Material properties (MPa)

f_y = MPa Yield strength for steel grade S355

E = MPa Modulus of elasticity for steel

Figure 1: Geometry

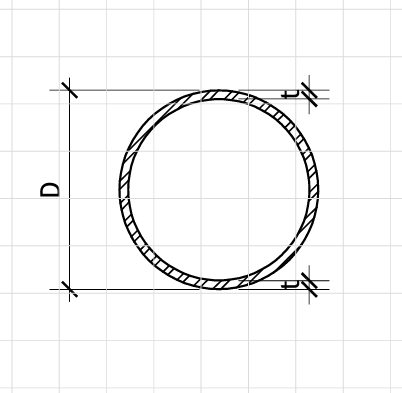
CHS-Section Dimensions

Applied design actions (kN, kNm)

N_ed = kN Axial force - positive for tension, negative for compression

V_ed = kN Shear force

M_ed = kNm Bending moment

Member properties

L = mm Member length (mm)

L_e/L = Effective length factor

L_e = 10000 mm Effective length (mm) for compression check

Partial safety factors

γ_m0 = For resistance of cross-sections

γ_m1 = For resistance of members to instability

CALCULATIONS

Geometric calculations

d_inner = D - 2×t = 72 mm

A = π×(D² - d_inner²)/4 = 464.96 mm² Gross cross-sectional Area

I = π×(D⁴ - d_inner⁴)/64 = 318495 mm⁴ Second Moment of Area

W_el = I/(D/2) = 8381.44 mm³ Elastic section modulus

W_pl = (D³ - d_inner³)/6 = 10954.7 mm³ Plastic section modulus

EC3-specific properties

ε = √(235/f_y) = 0.814

RESULTS

Section Properties

1. SECTION CLASSIFICATION (EN 1993-1-1, Table 5.2)

d/t = 38

Section Class: 2

Resistance Checks

2. CROSS-SECTIONAL RESISTANCE CHECKS (EN 1993-1-1, §6.2)

Axial Resistance

N_c,Rd = A×f_y/γ_m0 = 165.06 kN

Shear Resistance

A_v = 2×A/π = 296 mm²

V_pl,Rd = A_v×(f_y/√3)/γ_m0 = 60.67 kN

Bending Resistance

W_eff = W_pl = 10954.7 mm³

M_c,Rd = W_eff×f_y/γ_m0 = 3.89 kNm

Member Buckling

N_cr = π²×E×I/L_e² = 6.60 kN

λ̄ = √(A×f_y/N_cr) = 5.00

α = 0.21 Imperfection factor for CHS, curve a

φ = 0.5×(1 + α×(λ̄ - 0.2) + λ̄²) = 13.51

χ = 1/(φ + √(φ² - λ̄²)) = 0.038

N_b,Rd = χ×N_c,Rd = 6.34 kN

3. Combined Actions (EN 1993-1-1, §6.2.9 and §6.3.3)

Simplified check for combined actions. Full check requires complex Annex A or B factors.

--- Summary ---

Maximum ratio = 0.461