
🏗️ Frame Analysis Calculators
Structural analysis tools for various frame configurations and loading conditions.

Structural analysis tools for various frame configurations and loading conditions.
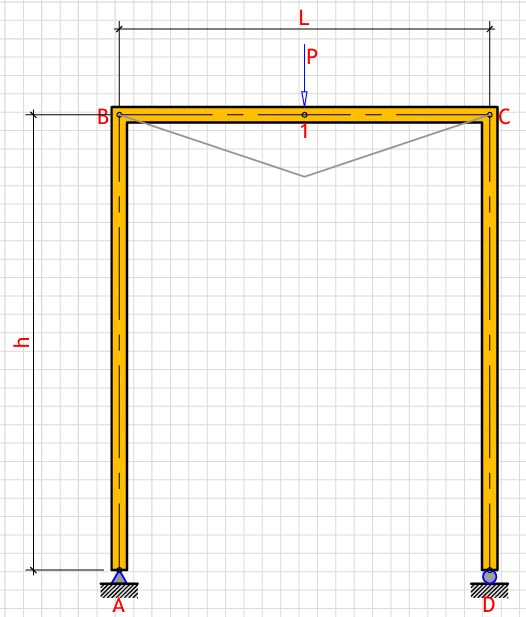
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_max (Maximum moment at point 1): - kN⋅m
δ_Dh (Horizontal displacement at point D): - mm
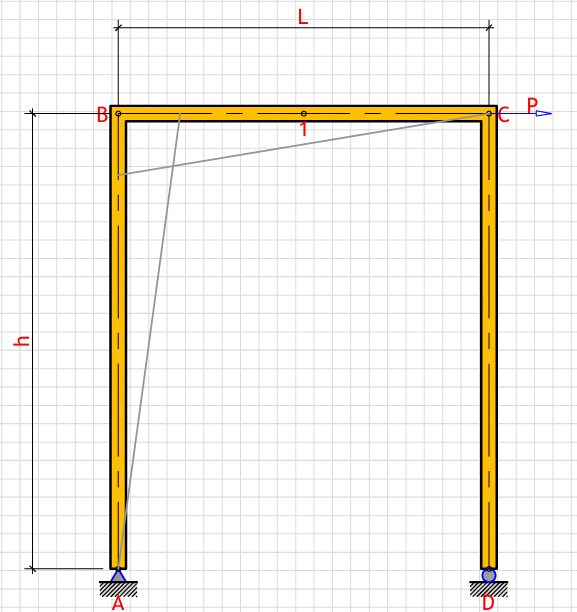
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_max (Maximum moment): - kN⋅m
δ_Ch (Horizontal displacement at point C): - mm
δ_Dh (Horizontal displacement at point D): - mm
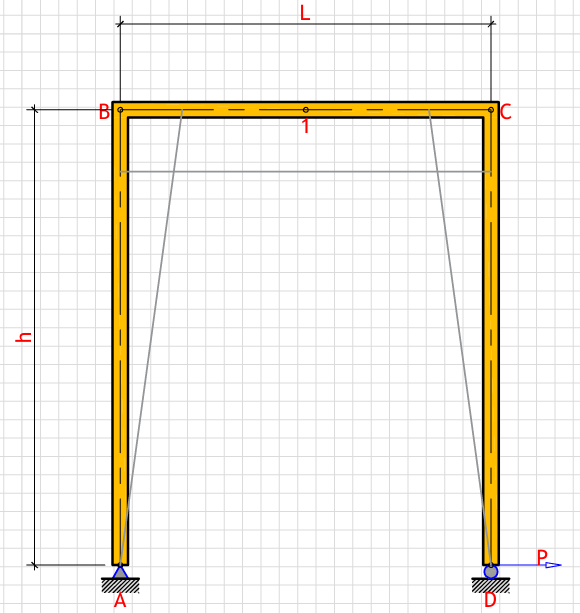
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_max (Maximum moment): - kN⋅m
δ_Dh (Horizontal displacement at point D): - mm
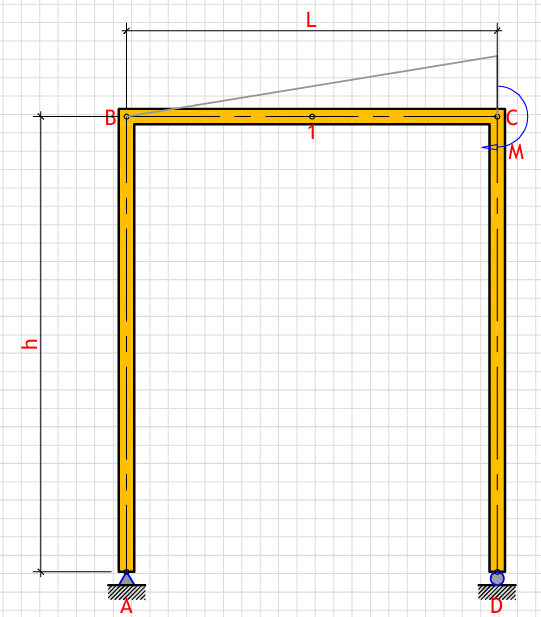
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_max (Maximum moment at points C): - kN⋅m
δ_Dh (Horizontal displacement at point D): - mm
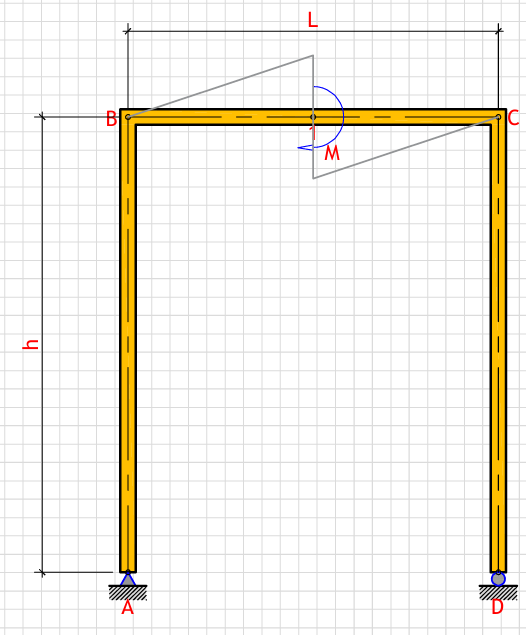
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_max (Maximum moment at points 1): - kN⋅m
θ_1 (Slope at point 1): - rad
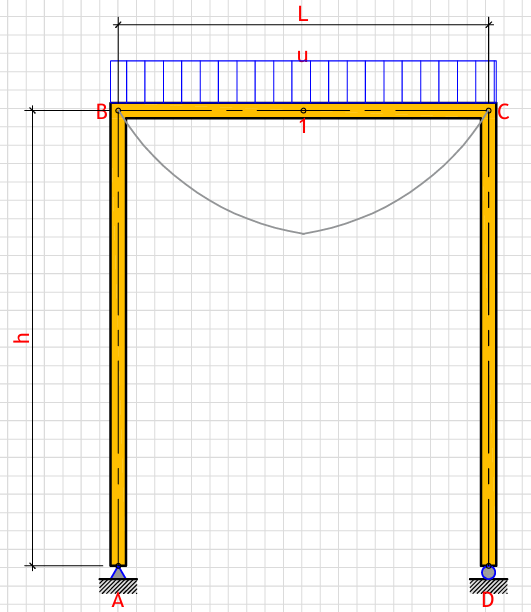
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_max (Maximum moment at point 1): - kN⋅m
δ_Dh (Horizontal displacement at point D): - mm
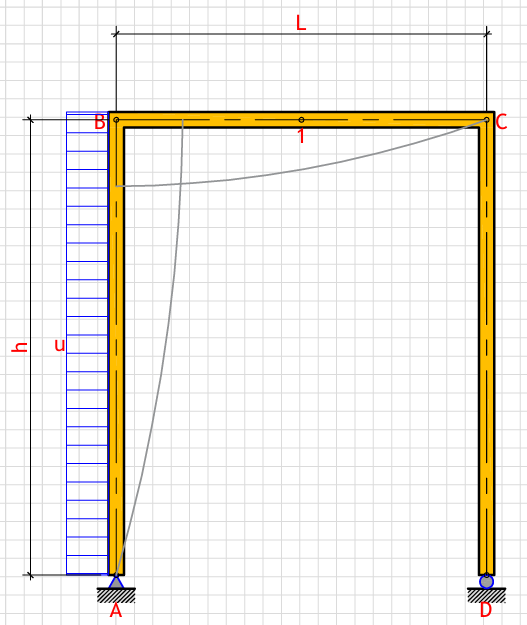
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_max (Maximum moment at point B): - kN⋅m
δ_Dh (Horizontal displacement at point D): - mm
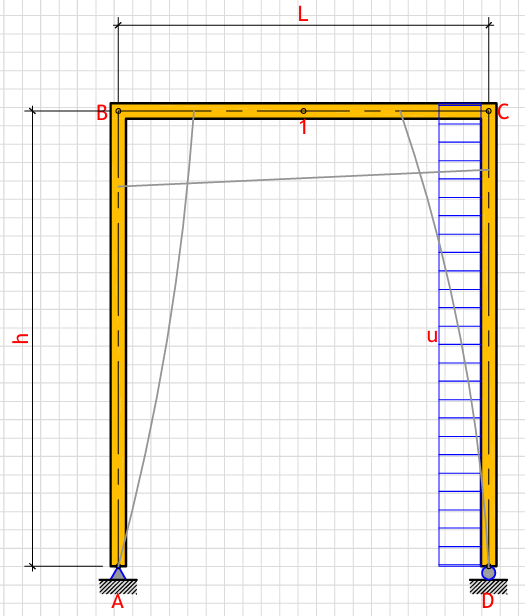
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
M_C (Moment at point C): - kN⋅m
M_max (Maximum moment at point B): - kN⋅m
δ_Dh (Horizontal displacement at point D): - mm
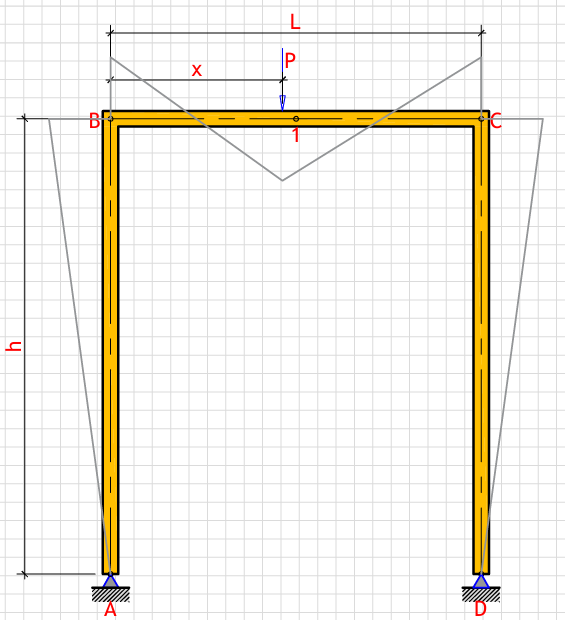
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
M_1 (Moment at point 1): - kN⋅m
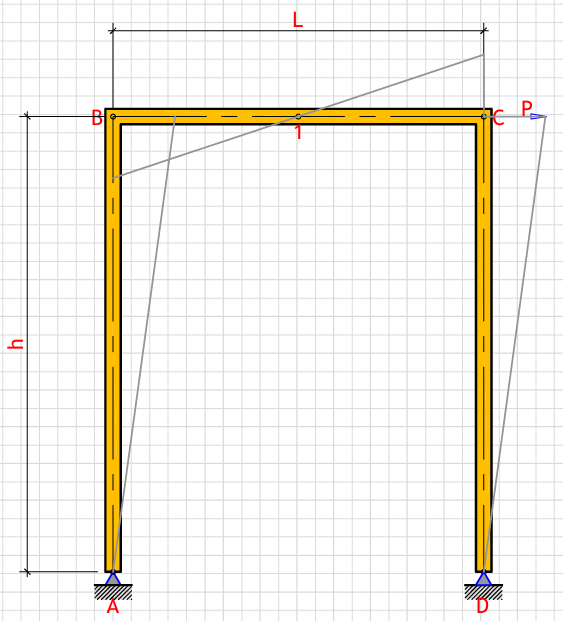
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
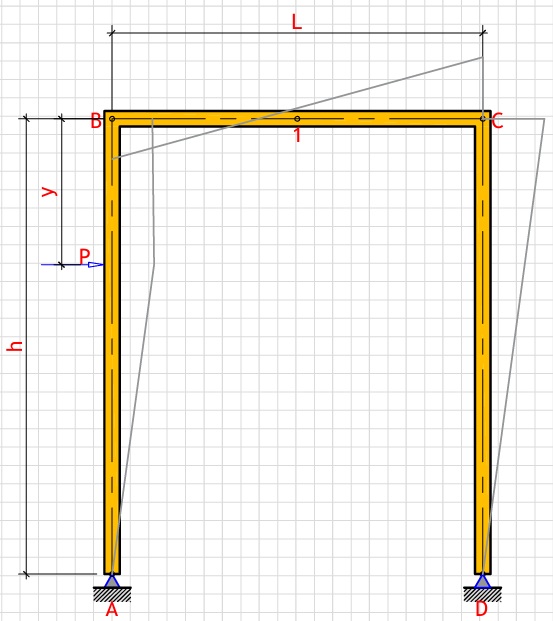
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_1 (Maximum moment at point 1): - kN⋅m
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
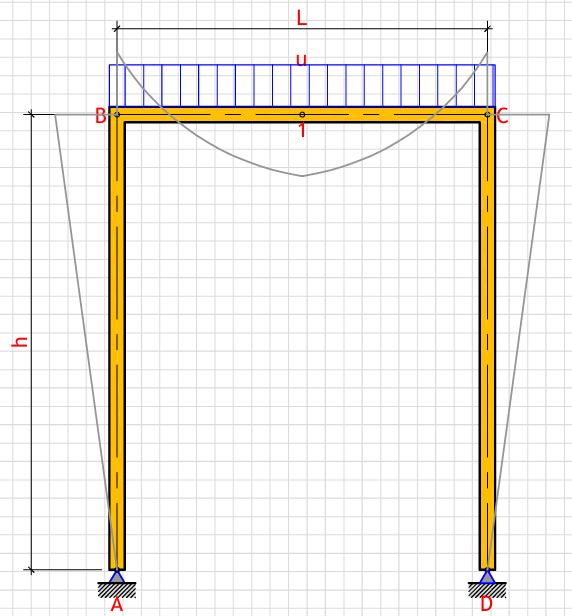
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_1 (Moment at point 1): - kN⋅m
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
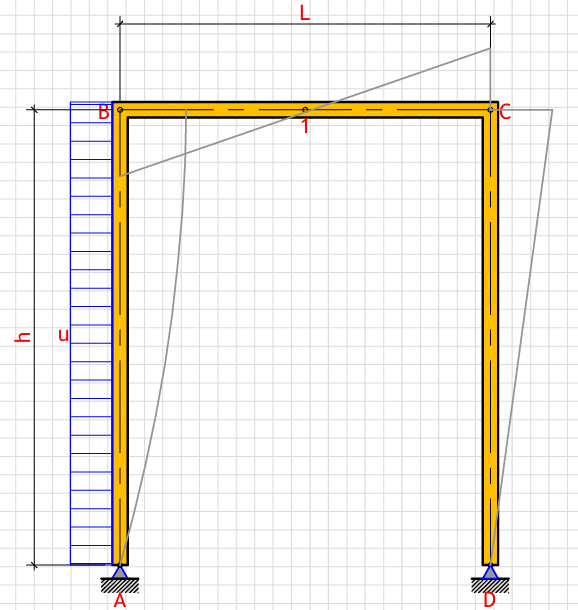
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
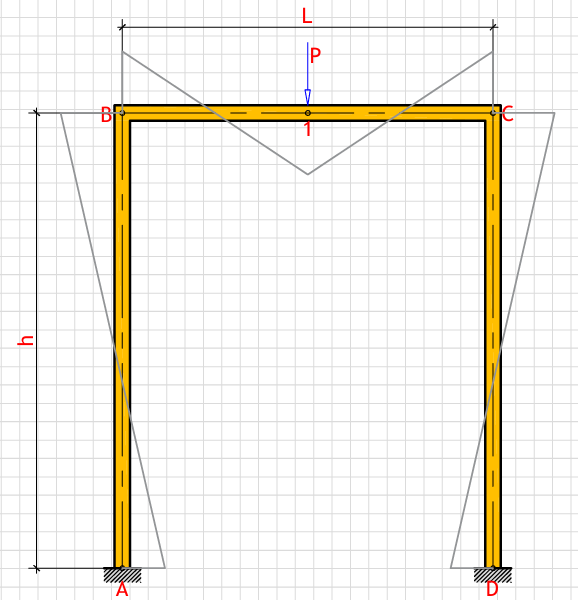
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_a (Moment at point A): - kN⋅m
M_b (Moment at point B & C): - kN⋅m
M_c (Moment at point C): - kN⋅m
M_d (Moment at point D): - kN⋅m
M_1 (Moment at point 1): - kN⋅m
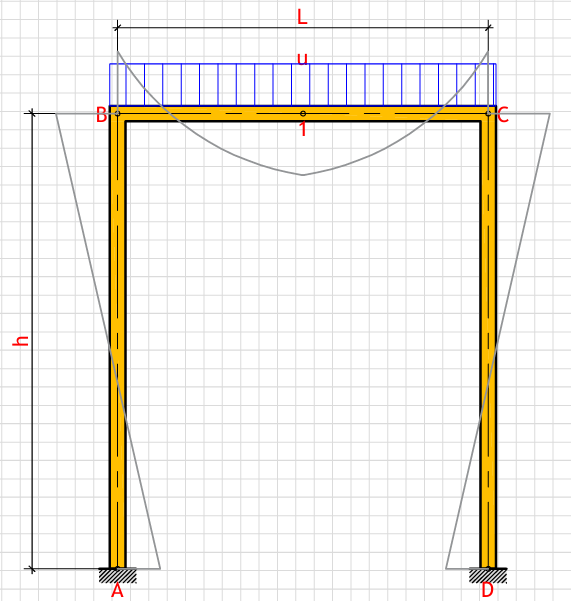
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_a (Moment at point A): - kN⋅m
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
M_d (Moment at point D): - kN⋅m
M_1 (Moment at point 1): - kN⋅m
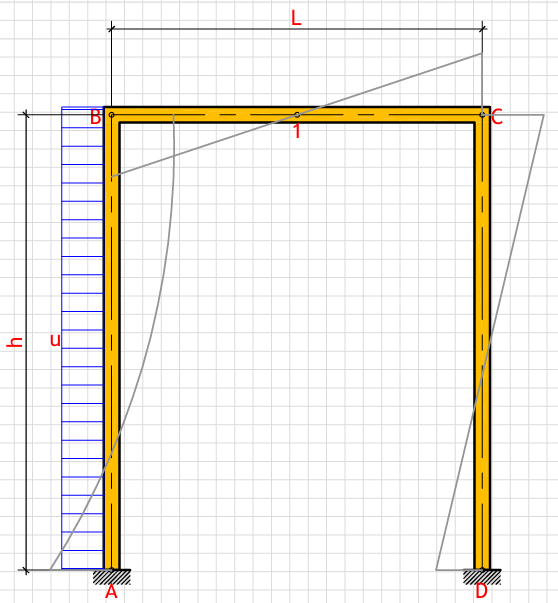
R_a (Left support vertical reaction): - kN
R_d (Right support vertical reaction): - kN
H_a (Left support horizontal reaction): - kN
H_d (Right support horizontal reaction): - kN
M_a (Moment at point A): - kN⋅m
M_b (Moment at point B): - kN⋅m
M_c (Moment at point C): - kN⋅m
M_d (Moment at point D): - kN⋅m
M_1 (Moment at point 1): - kN⋅m