DESIGN OF R.C. SOLID SLAB (ONE-WAY) - HK CoP 2013
1.0 INPUT DATA
Material Properties
fcu = MPa Characteristic concrete cube strength
fy = MPa Characteristic steel yield strength (Clause 3.2.1.1)
fy,comp = N/mm² Characteristic steel yield strength for
compression steel
γc = Partial safety factor for concrete
γs = Partial safety factor for steel
Ratiobasic = Basic span/effective depth ratio [Table 3.9]
Section Dimensions
L =
mm Effective span of slab
h =
mm Overall depth of slab
b =
mm Width of slab
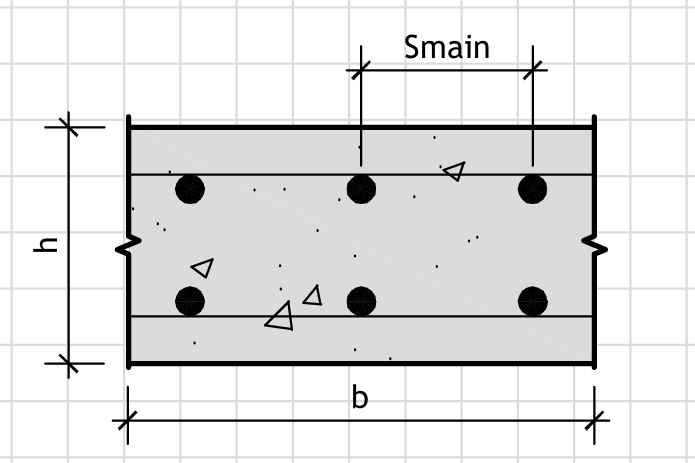
Figure 1: Geometry
RC Slab Dimensions
Loading
M =
kN·m Design ultimate moment
V =
kN Design ultimate shear force
Mservice = kN·m Service moment for deflection check
Assumed Reinforcement Sizes and Cover
cnom = mm Nominal cover
φmain = mm Main bar diameter
Smain = mm Main bar spacing
φcomp = mm Compression bar diameter (if needed)
φdist = mm Distribution bar diameter
2.0 CALCULATIONS
2.1 Ultimate Limit State (ULS) - Bending
Effective depth to tension steel
d = h − cnom −
φmain/2
d = 150 - 30 - 12/2 = 114.00 mm
Effective depth to compression steel
dcomp = cnom +
φcomp/2
dcomp = 30 + 10/2 = 35.00 mm
Step 1: Check if compression steel is required
K = M/(b·d²·fcu)
K = 26.9×10⁶/(1000×114²×45) = 0.0461
Kbal = 0.156 (Maximum K for singly reinforced
section)
Compression steel is NOT required (K < Kbal)
K' = 0.0461
Step 2: Calculate lever arm (z)
z = min(d·(0.5 + √(0.25 − K'/0.9)),
0.95·d)
z = min(114×(0.5 + √(0.25 - 0.0461/0.9)),
0.95×114)
z = 108.30 mm
Step 3: Calculate tension reinforcement (As)
As,req =
M/(fy/γs·z)
As,req = 26.9×10⁶/(500/1.15×108.30) =
571.48 mm²
Provide main bars (e.g. T12@150mm)
As,prov =
b·(φmain/2)²·π/Smain
As,prov = 1000×(12/2)²×π/150 = 753.98 mm² [in 1m width]
Step 4: Calculate compression reinforcement (As')
fcc = 0.45·fcu [Clause
4.3.2.1]
fcc = 0.45×45 = 20.25 MPa
x = d·(0.5 + √(0.25 − Kbal/0.9))
[Depth to neutral axis, using balanced condition]
x = 114×(0.5 + √(0.25 - 0.156/0.9)) = 0.00 mm
fs,comp = min(0.87·fy,comp,
700·(x − dcomp)/x)
fs,comp = min(0.87×500, 700×(0 -
35)/0) = 435.00 MPa
As',req = (K −
Kbal)·b·d²·fcu/(fs,comp·(d
− dcomp))
As',req = (0.0461 -
0.156)×1000×114²×45/(435×(114 - 35)) = 0.00 mm²
As,add,req =
As',req·fs,comp/(0.87·fy)
As,add,req = 0.00×435/(0.87×500) = 0.00 mm²
Provide compression bars (e.g. R10@300mm)
As',prov =
b·(φcomp/2)²·π/300 [R10@300mm in 1m width]
As',prov = 1000×(10/2)²×π/300
= 261.80 mm²
No compression steel required
As',req = 0 mm²
As',prov = 0 mm²
Check if tension reinforcement is sufficient
check_As = OK
(As,prov = 753.98 ≥
As,req = 571.48 mm²)
Check if compression reinforcement is sufficient
check_As' = OK
(Not required)
2.2 Ultimate Limit State (ULS) - Shear Check
Permissible shear stress in concrete
vc = 1
MPa·(0.79·(100·As,prov/(b·d))1/3·max(0.67,
(400/d·1 mm)1/4)·(fcu/25
MPa)1/3)/γc
vc = 1×(0.79×(100×753.98/(1000×114))¹ᐝ³·max(0.67,
(400/114)¹ᐝ⁴)·(45/25)¹ᐝ³)/1.25
vc = 0.583
MPa
Maximum shear stress [Clause 3.4.5.2]
vmax = min(0.8·√(fcu/1 MPa), 5)·1 MPa
vmax = min(0.8×√(45/1), 5)×1 = 5.000 MPa
Applied shear stress
v = V/(b·d)
v = 69.5×10³/(1000×114) = 0.610 MPa
Check shear stress
check_vmax = OK
(v = 0.610 ≤ vmax =
5.000 MPa)
check_vc = CHECK
(v = 0.610 > vc = 0.583 MPa)
Shear reinforcement is required
2.3 Serviceability Limit State (SLS) - Deflection Check
Modification factor for tension reinforcement
Factormod = min(0.55 + (477 MPa −
2·fy·As,req/(3·As,prov))/(120·(0.9 MPa
+ Mservice/(b·d²))), 2)
Factormod = min(0.55 + (477 -
2×500×571.48/(3×753.98))/(120×(0.9 + 26.9×10⁶/(1000×114²))), 2)
Factormod = 1.216
Allowable span/effective depth ratio
Ratioallow =
Ratiobasic·Factormod
Ratioallow = 23×1.216 = 27.97
Actual span/effective depth ratio
Ratioactual = L/d
Ratioactual = 2900/114 = 25.44
Check deflection
check_deflection = OK
(Ratioactual = 25.44 ≤
Ratioallow = 27.97)
*** OUTPUT SUMMARY ***
Design Summary
Effective depth, d = 114.00
mm
Lever arm, z = 108.30
mm
Required tension steel, As,req = 571.48 mm²
Provided tension steel, As,prov = 753.98 mm²
Tension reinforcement check: OK
Required compression steel (if needed), As',req = 0.00 mm²
Provided compression steel (if needed), As',prov = 0.00 mm²
Compression reinforcement check: OK
Design shear stress, v = 0.610
MPa
Allowable shear stress in concrete, vc = 0.583 MPa
Shear capacity check: CHECK - Shear reinforcement is required
Actual span/depth ratio, Ratioactual = 25.44
Allowable span/depth ratio, Ratioallow = 27.97
Deflection check: OK
RESULTS
DESIGN FAILS - SHEAR REINFORCEMENT REQUIRED