HKCoP 2013 PUNCHING SHEAR CHECK
1.0 INPUT DATA
Material Properties
fcu = MPa Characteristic concrete cube strength
fck = 0.8×fcu = 32.0 MPa Concrete characteristic cylinder strength
fy = MPa Reinforcement characteristic strength
γc = Partial safety factor for concrete
γs = Partial safety factor for reinforcement
Geometric Properties
h = mm Slab overall thickness
c =
mm Concrete cover
φb = mm Slab main bar diameter
c1 = mm Column dimension C1
c2 = mm Column dimension C2
ρl = % Flexural reinforcement ratio
VEd = kN Design shear force from analysis
Column Type Selection
Column Type = Select column location
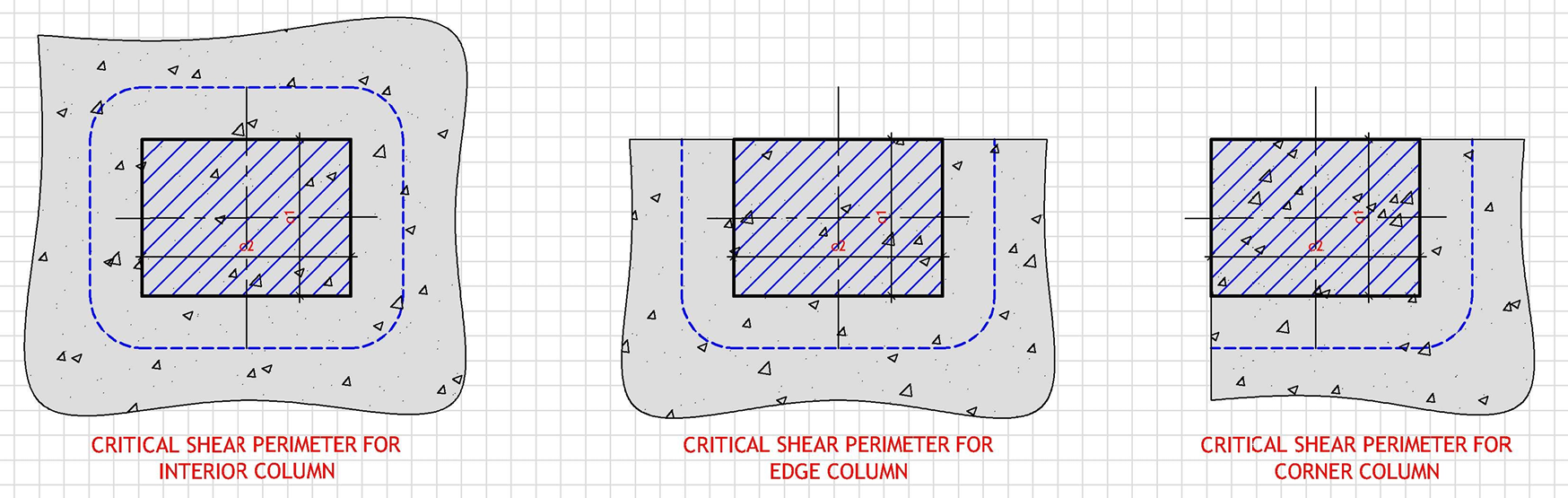
Figure 1: Geometry
Punching Shear Perimeter
2.0 CALCULATIONS
2.1 Effective Depths
Effective depth in X-direction (assume 20mm rebar)
deff,x = h − c −
0.5×φb
deff,x = 150 - 30 - 0.5×20 = 110.00 mm
Effective depth in Y-direction
deff,y = h − c −
1.5×φb
deff,y = 150 - 30 - 1.5×20 = 90.00 mm
Average effective depth
deff = (deff,x +
deff,y)/2
deff = (110.00 + 90.00)/2 = 100.00 mm
2.2 Column Parameters
Internal Column Parameters
β = 1.15 Enhancement factor for internal column
u0 = 2×(c1 +
c2) Perimeter at column face
u0 = 2×(300 + 300) = 1200.00 mm
u1 = 2×(c1 + c2) +
4×π×deff Basic control perimeter
u1 = 2×(300 + 300) + 4×π×100.00 = 2256.64 mm
Edge Column Parameters
β = 1.4 Enhancement factor for edge column
u0 = c1 + 2×c2
Perimeter at column face
u0 = 300 + 2×300 = 900.00 mm
u1 = 2×(c1 + 2×deff)
+ (c2 + 2×deff) Basic control
perimeter
u1 = 2×(300 + 2×100.00) + (300 +
2×100.00) = 1800.00 mm
Corner Column Parameters
β = 1.5 Enhancement factor for corner column
u0 = c1 + c2
Perimeter at column face
u0 = 300 + 300 = 600.00 mm
u1 = (c1 + 2×deff) +
(c2 + 2×deff) + π×deff
Basic control perimeter
u1 = (300 + 2×100.00) + (300 +
2×100.00) + π×100.00 = 1714.16
mm
2.3 Check max shear stress at column face (u₀)
Design concrete strength
fcd = fck/γc
fcd = 32.0/1.5 = 21.33 MPa
Conversion factor Eurocode 2
αcc = 1
Max shear resistance
vRd,max = 0.4×(1 −
(fck/1MPa)/250)×αcc×fcd
vRd,max = 0.4×(1 − 32/250)×1×21.33 =
7.49 MPa
Applied shear stress
vEd,max =
β×VEd/(u0×deff)
vEd,max = 1.15×200×10³/(1200.00×100.00) = 1.917 MPa
Maximum Stress Check
check_max_stress = PASS
(vEd,max = 1.917 ≤
vRd,max = 7.49 MPa)
2.4 Check shear stress at basic control perimeter (u₁)
Size effect factor
k = min(2.0; 1 + √(200/(deff/1mm)))
k = min(2.0; 1 + √(200/100.00)) = 2.414
Minimum shear strength
vmin =
0.035×k3/2×√(fck/1MPa)×1MPa
vmin = 0.035×2.414³ᐟ²×√32 = 0.485 MPa
Shear resistance of concrete
vRd,c =
0.18/γc×k×(100×ρl×fck/1MPa)1/3×1MPa
vRd,c = 0.18/1.5×2.414×(100×1×32)¹ᐟ³ =
0.485 MPa
(Take vmin as minimum requirement)
Applied shear stress at basic perimeter
vEd,u1 =
β×VEd/(u1×deff)
vEd,u1 = 1.15×200×10³/(2256.64×100.00)
= 1.020 MPa
Basic Perimeter Check
check_basic_perimeter = SHEAR REINFORCEMENT
REQUIRED
(vEd,u1 = 1.020 >
vRd,c = 0.485 MPa)
2.5 Design Punching Shear Reinforcement
Effective design strength of reinforcement
fywd,ef =
min((fy/1MPa)/γs; 250 +
0.25×(deff/1mm))×1MPa
fywd,ef = min(500/1.15; 250 +
0.25×100.00) = 434.78 MPa
Maximum radial spacing
sr = 0.75×deff
sr = 0.75×100.00 = 75.00 mm
Required area of shear reinforcement
Asw,required = max(0mm²; (vEd,u1 −
vRd,c)×sr×u1/(1.5×fywd,ef))
Asw,required = (1.020 -
0.485)×75.00×2256.64/(1.5×434.78) = 490.65 mm²
No shear reinforcement required
Asw,required = 0
mm²
*** OUTPUT SUMMARY ***
Design Summary
Column Type = Internal
Enhancement Factor β = 1.15
Effective depth deff = 100.00 mm
Perimeter at column face u0 = 1200.00 mm
Basic control perimeter u1 = 2256.64 mm
Max shear resistance vRd,max = 7.49 MPa
Applied max shear stress vEd,max = 1.917 MPa
Max stress check: PASS
Concrete shear resistance vRd,c = 0.485 MPa
Applied shear stress vEd,u1 = 1.020 MPa
Basic perimeter check: SHEAR REINFORCEMENT REQUIRED
Required shear reinforcement Asw,required = 490.65 mm²
RESULTS
DESIGN REQUIRES SHEAR REINFORCEMENT